Read Data
The data for the multiple linear regression model are stored in a CSV file and an R data file. We can read the data using appropriate methods.
read.csv()
Use read.csv()
= read.csv ("Data/teamData_2001_to_2020.csv" )head (team_data)
yearID lgID teamID franchID divID Rank G Ghome W L DivWin WCWin LgWin
1 2001 AL TBA TBD E 5 162 81 62 100 N N N
2 2001 AL BAL BAL E 4 162 80 63 98 N N N
3 2001 AL KCA KCR C 5 162 81 65 97 N N N
4 2001 AL DET DET C 4 162 81 66 96 N N N
5 2001 AL TEX TEX W 4 162 82 73 89 N N N
6 2001 AL ANA ANA W 3 162 81 75 87 N N N
WSWin R AB H X2B X3B HR BB SO SB CS HBP SF RA ER ERA CG SHO SV
1 N 672 5524 1426 311 21 121 456 1116 115 52 54 25 887 781 4.94 1 6 30
2 N 687 5472 1359 262 24 136 514 989 133 53 77 49 829 744 4.67 10 6 31
3 N 729 5643 1503 277 37 152 406 898 100 42 44 47 858 779 4.87 5 1 30
4 N 724 5537 1439 291 60 139 466 972 133 61 51 49 876 795 5.01 16 2 34
5 N 890 5685 1566 326 23 246 548 1093 97 32 75 55 968 913 5.71 4 3 37
6 N 691 5551 1447 275 26 158 494 1001 116 52 77 53 730 671 4.20 6 1 43
IPouts HA HRA BBA SOA E DP FP name
1 4271 1513 207 569 1030 139 144 0.977 Tampa Bay Devil Rays
2 4297 1504 194 528 938 125 137 0.979 Baltimore Orioles
3 4320 1537 209 576 911 117 204 0.981 Kansas City Royals
4 4288 1624 180 553 859 131 164 0.979 Detroit Tigers
5 4315 1670 222 596 951 114 167 0.981 Texas Rangers
6 4313 1452 168 525 947 103 142 0.983 Anaheim Angels
park attendance BPF PPF teamIDBR teamIDlahman45
1 Tropicana Field 1298365 98 100 TBD TBA
2 Oriole Park at Camden Yards 3094841 95 96 BAL BAL
3 Kauffman Stadium 1536371 107 108 KCR KCA
4 Comerica Park 1921305 93 95 DET DET
5 The Ballpark at Arlington 2831021 104 105 TEX TEX
6 Edison International Field 2000919 101 101 ANA ANA
teamIDretro X1B TB RPG AVG SLG OBP RC
1 TBA 973 2142 4.148148 0.2581463 0.3877625 0.3195247 163.5749
2 BAL 937 2077 4.240741 0.2483553 0.3795687 0.3190445 178.5728
3 KCA 1037 2310 4.500000 0.2663477 0.4093567 0.3180782 155.2923
4 DET 949 2267 4.469136 0.2598880 0.4094275 0.3204981 176.2221
5 TEX 971 2676 5.493827 0.2754617 0.4707124 0.3440201 235.5229
6 ANA 988 2248 4.265432 0.2606738 0.4049721 0.3268016 183.9469
OPS
1 0.7072872
2 0.6986132
3 0.7274349
4 0.7299256
5 0.8147325
6 0.7317737
[1] "yearID" "lgID" "teamID" "franchID"
[5] "divID" "Rank" "G" "Ghome"
[9] "W" "L" "DivWin" "WCWin"
[13] "LgWin" "WSWin" "R" "AB"
[17] "H" "X2B" "X3B" "HR"
[21] "BB" "SO" "SB" "CS"
[25] "HBP" "SF" "RA" "ER"
[29] "ERA" "CG" "SHO" "SV"
[33] "IPouts" "HA" "HRA" "BBA"
[37] "SOA" "E" "DP" "FP"
[41] "name" "park" "attendance" "BPF"
[45] "PPF" "teamIDBR" "teamIDlahman45" "teamIDretro"
[49] "X1B" "TB" "RPG" "AVG"
[53] "SLG" "OBP" "RC" "OPS"
load()
Use load() teamData
load ("Data/teamData_2001_to_2020.RData" )head (teamData)
yearID lgID teamID franchID divID Rank G Ghome W L DivWin WCWin LgWin
1 2001 AL TBA TBD E 5 162 81 62 100 N N N
2 2001 AL BAL BAL E 4 162 80 63 98 N N N
3 2001 AL KCA KCR C 5 162 81 65 97 N N N
4 2001 AL DET DET C 4 162 81 66 96 N N N
5 2001 AL TEX TEX W 4 162 82 73 89 N N N
6 2001 AL ANA ANA W 3 162 81 75 87 N N N
WSWin R AB H X2B X3B HR BB SO SB CS HBP SF RA ER ERA CG SHO SV
1 N 672 5524 1426 311 21 121 456 1116 115 52 54 25 887 781 4.94 1 6 30
2 N 687 5472 1359 262 24 136 514 989 133 53 77 49 829 744 4.67 10 6 31
3 N 729 5643 1503 277 37 152 406 898 100 42 44 47 858 779 4.87 5 1 30
4 N 724 5537 1439 291 60 139 466 972 133 61 51 49 876 795 5.01 16 2 34
5 N 890 5685 1566 326 23 246 548 1093 97 32 75 55 968 913 5.71 4 3 37
6 N 691 5551 1447 275 26 158 494 1001 116 52 77 53 730 671 4.20 6 1 43
IPouts HA HRA BBA SOA E DP FP name
1 4271 1513 207 569 1030 139 144 0.977 Tampa Bay Devil Rays
2 4297 1504 194 528 938 125 137 0.979 Baltimore Orioles
3 4320 1537 209 576 911 117 204 0.981 Kansas City Royals
4 4288 1624 180 553 859 131 164 0.979 Detroit Tigers
5 4315 1670 222 596 951 114 167 0.981 Texas Rangers
6 4313 1452 168 525 947 103 142 0.983 Anaheim Angels
park attendance BPF PPF teamIDBR teamIDlahman45
1 Tropicana Field 1298365 98 100 TBD TBA
2 Oriole Park at Camden Yards 3094841 95 96 BAL BAL
3 Kauffman Stadium 1536371 107 108 KCR KCA
4 Comerica Park 1921305 93 95 DET DET
5 The Ballpark at Arlington 2831021 104 105 TEX TEX
6 Edison International Field 2000919 101 101 ANA ANA
teamIDretro X1B TB RPG AVG SLG OBP RC
1 TBA 973 2142 4.148148 0.2581463 0.3877625 0.3195247 163.5749
2 BAL 937 2077 4.240741 0.2483553 0.3795687 0.3190445 178.5728
3 KCA 1037 2310 4.500000 0.2663477 0.4093567 0.3180782 155.2923
4 DET 949 2267 4.469136 0.2598880 0.4094275 0.3204981 176.2221
5 TEX 971 2676 5.493827 0.2754617 0.4707124 0.3440201 235.5229
6 ANA 988 2248 4.265432 0.2606738 0.4049721 0.3268016 183.9469
OPS
1 0.7072872
2 0.6986132
3 0.7274349
4 0.7299256
5 0.8147325
6 0.7317737
[1] "yearID" "lgID" "teamID" "franchID"
[5] "divID" "Rank" "G" "Ghome"
[9] "W" "L" "DivWin" "WCWin"
[13] "LgWin" "WSWin" "R" "AB"
[17] "H" "X2B" "X3B" "HR"
[21] "BB" "SO" "SB" "CS"
[25] "HBP" "SF" "RA" "ER"
[29] "ERA" "CG" "SHO" "SV"
[33] "IPouts" "HA" "HRA" "BBA"
[37] "SOA" "E" "DP" "FP"
[41] "name" "park" "attendance" "BPF"
[45] "PPF" "teamIDBR" "teamIDlahman45" "teamIDretro"
[49] "X1B" "TB" "RPG" "AVG"
[53] "SLG" "OBP" "RC" "OPS"
Check the Data
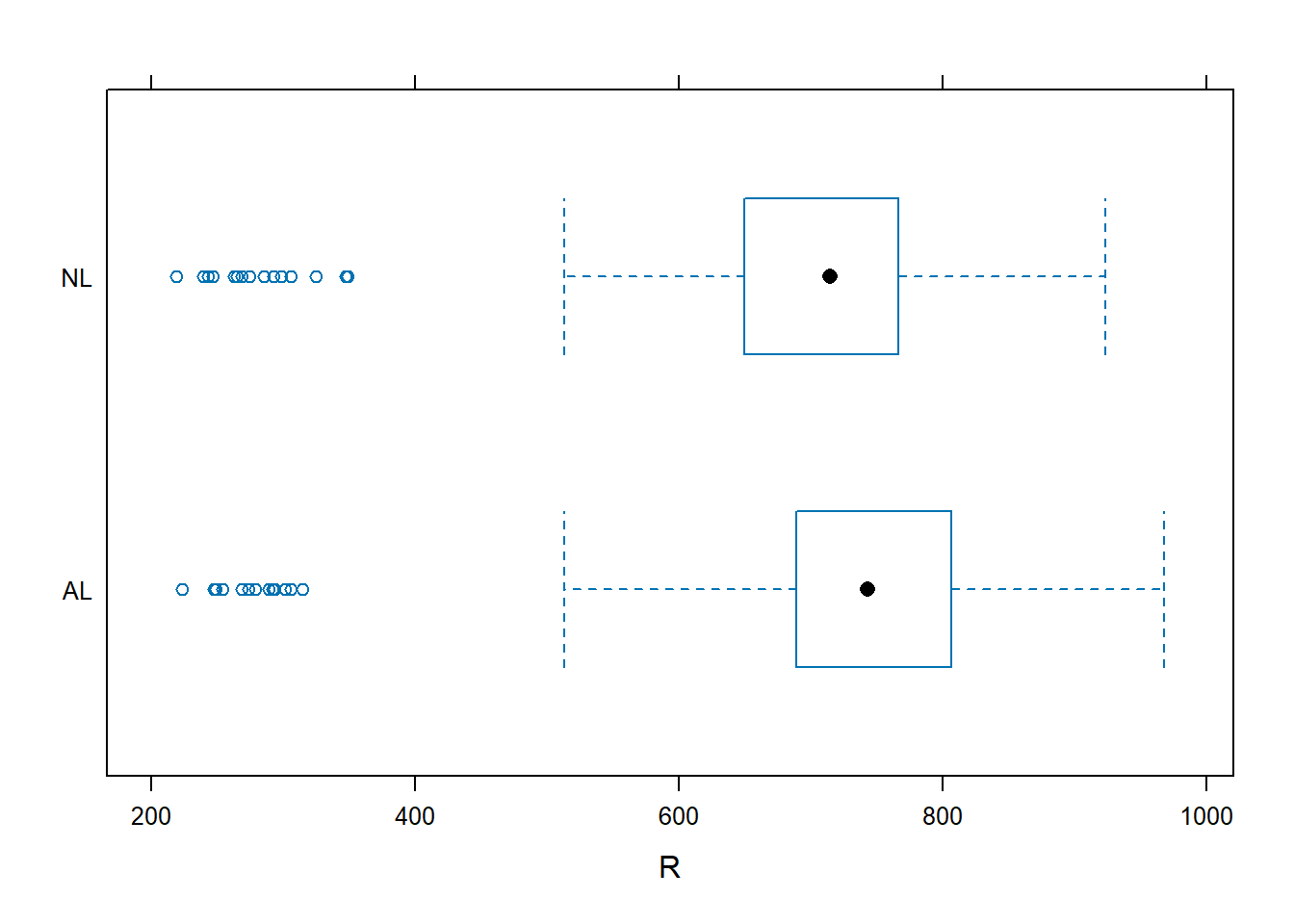
We perform a quick plot to see if things look okay. We also look at a simple MLR model and determine the MSE.
bwplot (lgID ~ R, data= teamData)= lm (R ~ H + BB, data= teamData)summary (teamData.lm.r.h.bb)
Call:
lm(formula = R ~ H + BB, data = teamData)
Residuals:
Min 1Q Median 3Q Max
-138.433 -32.288 1.632 31.545 159.549
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -33.21556 12.33483 -2.693 0.00728 **
H 0.37142 0.01248 29.773 < 2e-16 ***
BB 0.46071 0.02921 15.774 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 47.11 on 597 degrees of freedom
Multiple R-squared: 0.8634, Adjusted R-squared: 0.863
F-statistic: 1887 on 2 and 597 DF, p-value: < 2.2e-16
anova (teamData.lm.r.h.bb)
Analysis of Variance Table
Response: R
Df Sum Sq Mean Sq F value Pr(>F)
H 1 7825448 7825448 3525.51 < 2.2e-16 ***
BB 1 552298 552298 248.82 < 2.2e-16 ***
Residuals 597 1325141 2220
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
= rev (anova (teamData.lm.r.h.bb)$ "Mean Sq" )[1 ]= sqrt (MSE)
So, for the model fitting R H BB mean squared error is MSE = 2219.666, and the root mean squared error is RMSE = 47.1133.