
I've worked on a variety of projects, some with colleagues, some with students, and some on my own.
Surface Science: Scanning Tunneling Microscopy

STM image of the Si(001) - 2×1 surface. Each diagonal stripe is two atoms wide. Four planes of the silicon crystal are revealed; the upper plane is in the lower left of the image, and the lower is in the upper right corner.
In graduate school, I was trained as a Condensed Matter Physicist, specializing in Surface Science. There, I primarily did Scanning Tunneling Microscopy (STM) under ultra-high vacuum conditions to investigate the interactions of surfaces and adsorbates and to manipulate those interactions via nanolithography; Low Energy Electron Diffraction (LEED), Auger Spectroscopy, and Mass Spectroscopy were additional tools for interpreting our STM images and atom-tracking data. In Eric Ganz's lab in the physics department of the University of Minnesota, I worked on a number of projects investigating atomic surface-diffusion, nanofabrication and chemical and physical vapor deposition.
At the University of Redlands, I've worked with students to construct a new STM with which to continue this work.
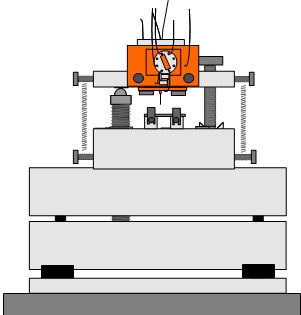
With a more pedagogical focus, I've also worked with a student on an update of the minimalistic "homebrew STM" that might be used in our Advanced Lab to demonstrate the principles of STM operation as well as the central feature of quantum mechanical tunneling (which puts the T in STM).
Adsorption of
TiCl4 and initial stages of Ti growth on Si(001),
T. Mitsui, E. Hill, R. Curtis, and E. Ganz.
Journal of Vacuum Science and Technology A
19, 563 (2000).
Hydrogen diffusion
on the Si(001) surface studied by Atom Tracking,
E. Hill, B. Freelon,
and E. Ganz. Physical Review B 60, 15896 (1999).
Nanolithography by
selective chemical vapor deposition with an atomic hydrogen resist,
T. Mitsui, E. Hill,
and E. Ganz. Journal of Applied Physics
85, 522 (1999).
Initial stages of Al
growth from dimethylaluminum hydride,
T. Mitsui, E. Hill, R. Curtis, and E. Ganz. Physical Review
B 59, 8123 (1999).

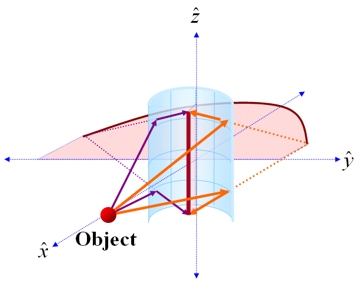

Initially intrigued by the optics of a helical mirror, I was able tcollaboratecollaborate with Dr. DeWeerd in exploring the optics of some interesting surfaces and how they might be discussed in terms of the optics that introductory students learn. The corner mirror, cylindrical mirror are (in education speak) scaffolding for approaching the helical mirror. This work prepared us for related detours into the complications of anamorphic images, and the every-day observation of reflections from liquid (say, beverage) surfaces.

Coffee Cup
Reflection
with a Twist:
the Helical Mirror.
A. J. DeWeerd and
Comment on
‘Anamorphic Images,’ by J.L. Hunt, B.G. Nickel, and Christian Gigault [Am. J.
Phys. 68 (3), 232-237 (2000)].
A.
J. DeWeerd and S. E. Hill. Am. J.
Phys. 74 (1), 83-84 (2006).
Optics Over Tea:
Images in Concave and Convex Surfaces,
A. J. DeWeerd and S.
E. Hill. Physics Education 40 (1),
13-14(2005).
The Dizzying Depths
of Cylindrical Mirrors,
A. J. DeWeerd and S.
E. Hill. The Physics Teacher
43 (2), 90-92 (2005).
First as a student, and then as an instructor, I was confused by and dissatisfied with the typical discussions of Faraday's Law and the Maxwell-Ampere Law, which suggests that the behavior of one type of field is caused by the behavior of the other. So, in preparation for teaching our upper-level Electricity and Magnetism course, I set myself the goal of really understanding these laws. Reading the literature, I realized that physical arguments demonstrate, indeed most physicists and even historians and philosophers of physics who seriously consider these laws agree, that this suggestion is incorrect. Having deepend my own understanding of Maxwell-Ampere and Faraday's laws, I wrote two papers to share the existing evidence and arguments with students and teachers (and text writers) of introductory physics.
Reanalyzing the
Ampere-Maxwell Law.
S. Eric Hill. The Physics
Teacher 49 (6), 343-345 (2011).
Rephrasing Faraday’s
Law.
S. Eric Hill.
The Physics Teacher 48 (6),
410-412 (2010).
Sometimes, after a work has been published, you find new results or resources that you wish you could have included. Here are two that I would have cited in these papers if I'd found them in time:
O D Jefimenko, "Presenting electromagnetic theory in accordance with the principle of causality." Eur. J. Phys. 24 287-296 (2004).
While my two papers draw heavily from other works by Jefimenko, this one is particularly relevant and I somehow missed it.
J. D. Jackson, "Reply to Comment by J. Roche on 'Maxwell's displacement current revisited'", Eur. J. Phys. 21, L29-L30 (2000).
Jackson makes an important point about the distinction between what we mean by a mathematical source (information from which we deduce further information) vs. a physical source (situation which causes another situation.) For example, an outfielder's catching a ball is a source of our knowledge that the batter hit, but is not what caused the ball to be hit. Miscommunications and misunderstandings about the laws may follow from our seldom specifying which sense in which we're using the term "source."
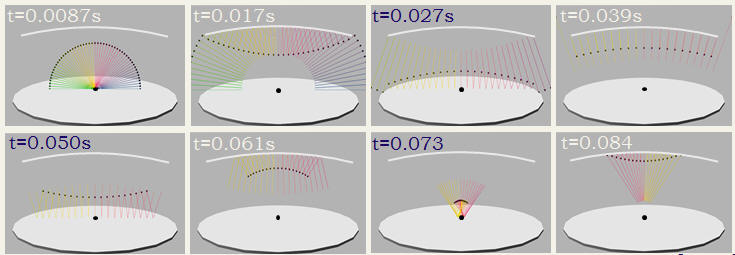
When my department moved into our new facility, we were greeted by a science-museum-worthy, acoustically 'live' entry porch. A student and I set about understanding the porch's echo so we could design a placard that explains it to curious visitors. In short, the domed ceiling and hard surfaces supported a tremendous flutter echo that, refocuses in the center every third echo, giving a waltz-like beat. The dome proved an excellent test case for modeling and understanding a variety of acoustic phenomenon, many of which are handled in professional room-acoustics packages using ray acoustics (akin to ray optics): the echo's period, the decay-time, the 'brightening' of the sound as lower frequencies are preferentially absorbed, etc. With other students I've explored other computational approaches, like finite-difference, and more analytical approaches like transfer matrix and solving the wave equation for resonances (quite similar to those for a kettle drum.)
While this work has been featured in students' research posters, papers, and presentations, I've not published any of it.
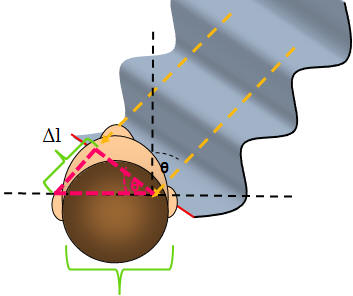
Starting with a Visiting Professorship at St. Olaf when I was ABD (all but dissertation), I've taught a general-ed "Sound Physics" or "Musical Acoustics" course a number of times over the years. There are a number of common physics experiments for such a class (like resonances on a string), but I've also develop a number of experiments, with students and on my own, to support that class by connecting tangible phenomenon with the abstract ideas and tools of physics. For example, the combination of acoustic cues we unconsciously use to identify the location of a sound source.
While this work has been featured in students' research posters, papers, and presentations, I've not published any of it.